Doce científicos que quizás no conoces pero que hicieron grandes aportes a la Física

Albert Einstein es el físico por excelencia, y nombres como Copérnico, Galileo, Newton, Curie, Sagan o Hawking también resultan familiares para muchos. Sin embargo, la lista de personas que han realizado contribuciones revolucionarias, no solo a la física, sino a nuestra comprensión del universo, es mucho más extensa. En este artículo, exploraremos brevemente las aportaciones de doce científicos destacados, aunque menos conocidos, y el fascinante recorrido que los llevó a seis de los descubrimientos más espectaculares en la historia de la física.

1. Tycho Brahe y Johannes Kepler

A pesar de que usualmente el sistema del universo heliocéntrico se asocia con Nicolás Copérnico, si a la larga este prevaleció, destronando el modelo geocéntrico de Ptolomeo después de casi quince siglos de uso para la predicción de eventos astronómicos, fue gracias a las observaciones de Tycho Brahe y al trabajo espectacular de Johannes Kepler.

Tycho Brahe nació en 1546 en una familia noble en Dinamarca y mostró un temprano interés por las ciencias, especialmente la astronomía. Primero desde su observatorio en la isla de Hven, el Uraniborg o templo de Urania, y posteriormente desde Praga, dedicó su vida al refinamiento y diseño de nuevos instrumentos y métodos de observación astronómica, que le permitieron obtener mediciones de las posiciones de los planetas y las estrellas con una precisión sin precedentes para su época.

Aunque Tycho no era heliocentrista, al morir en 1601 legó los datos que acumuló a lo largo de varias décadas sobre la posición del planeta Marte relativa a la Tierra a su asistente Johannes Kepler (1571, Weil der Stadt - 1630, Regensburg, Alemania). Kepler era en ese momento un joven matemático partidario de la teoría de Copérnico y pretendía encontrar un modelo geométrico para describir la estructura del universo en cuya sencillez y elegancia pudiera reconocerse la grandeza de Dios.

Medio siglo después, las Leyes de Kepler proveyeron de sostén empírico a la mecánica de Newton, ya que Newton fue capaz de derivarlas matemáticamente a partir de su Ley de Gravitación Universal, reproduciendo de manera teórica las conclusiones a las que Kepler arribó de forma empírica. En la actualidad, estas leyes siguen siendo fundamentales en la astronomía, siendo esenciales para la planificación de misiones espaciales, el estudio de exoplanetas y la detección de ondas gravitacionales emitidas durante colisiones entre estrellas de neutrones y agujeros negros.

A pesar del enorme alcance científico y cultural de su descubrimiento, Kepler vivió frustrado al no poder explicar por qué la naturaleza había elegido órbitas elípticas en lugar de circulares, que él consideraba más sencillas desde el punto de vista matemático y más "perfectas" en un sentido filosófico. Gracias al desarrollo de mejores métodos de observación astronómica y de teorías más precisas, hoy sabemos que en el espacio tridimensional las órbitas de los planetas no son cerradas, por tanto, no son rigurosamente elípticas. Sin embargo, puede decirse que la suposición de Kepler de que las órbitas son las curvas más sencillas posibles sí se ha visto confirmada, pues en el espacio-tiempo cuatridimensional de la Teoría de la Relatividad General los planetas se mueven siguiendo unas curvas llamadas geodésicas, que en lenguaje mundano es como decir que describen las trayectorias más simples posibles.

2. Joseph-Louis Lagrange y William Rowan Hamilton

Aunque de manera superficial tanto el enfoque de Lagrange como el de Hamilton pueden verse como formas distintas de expresar una misma teoría, con el tiempo se revelaron como dos herramientas matemáticas poderosísimas. En primer lugar, ambos enfoques simplificaron y generalizaron la descripción de los sistemas mecánicos, permitiendo la resolución de muchos problemas concretos que desde el punto de vista newtoniano eran extremadamente difíciles de tratar. Pero su mayor relevancia radica en que ambos evolucionaron hasta convertirse en métodos para describir teóricamente cualquier sistema físico. En las mecánicas de Lagrange y Hamilton, toda la información de un sistema queda codificada en el lagrangiano o el hamiltoniano, de los cuales pueden derivarse sus ecuaciones de movimiento, es decir, la expresión matemática de las leyes físicas que lo rigen. Por ejemplo, si uno conoce el lagrangiano (o hamiltoniano) del electromagnetismo, puede obtener de él las ecuaciones de Maxwell; mientras que si conoce el de la Relatividad General, puede obtener las ecuaciones de Einstein.

Por supuesto, los lagrangianos y hamiltonianos deben ser conocidos, pero estos pueden construirse siguiendo una serie de reglas básicas de la física, de conjunto con las observaciones y experimentos disponibles en un momento dado. De esta manera, a principios del siglo pasado, el formalismo de Hamilton hizo posible la transición de la Mecánica Clásica a la Cuántica, mientras que el de Lagrange permitió, entre las décadas de 1950 y 1970, la unificación de la Relatividad Especial y la Mecánica Cuántica en la Teoría de Campos, y la construcción del Modelo Estándar que describe las interacciones electromagnética, débil y fuerte en el marco de la física de partículas. Estos enfoques no solo permitieron modelar lo ya conocido, sino que también facilitaron la predicción de nuevas partículas y fenómenos.

3. Emmy Noether (1882, Erlangen, Alemania- 1935, Bryn Mawr, Pensilvania, Estados Unidos)

Este resultado es uno de los más profundos y bellos de la física, pues pone de manifiesto la conexión para nada evidente que existe entre las cantidades observables de un sistema y su descripción matemática abstracta, al tiempo que aporta un método para la determinación y estudio de dichas cantidades. Además, complementa los métodos de Lagrange y Hamilton, ya que para saber las simetrías de un sistema basta con estudiar las propiedades matemáticas de su lagrangiano, o hamiltoniano. Por eso, de conjunto con ellos, se ha convertido en una de las herramientas principales sobre la que se erige actualmente la física de partículas, sirviendo de guía para la extensión de las teorías existentes y el diseño de experimentos que permitan aceptar o descartar dichas extensiones. De esta forma, el teorema de Noether fue sido crucial, por ejemplo, en la observación experimental del bosón de Higgs en 2012, y continúa siendo una herramienta fundamental en teorías como la supersimetría, que buscan ampliar los horizontes de la física más allá del Modelo Estándar.

Aunque hoy en día tanto la ciencia como la ciencia ficción se han encargado de popularizar esas extraordinarias imágenes de las galaxias y otros objetos astronómicos que pueblan el vastísimo y aún muy desconocido espacio exterior a nuestro planeta, hace apenas cien años la humanidad creía que el universo se reducía a la Vía Láctea. Fue el abogado y astrónomo estadounidense Edwin Hubble quien, desde el Observatorio de Monte Wilson en California, descubrió hacia mitad de la década de 1920 que el universo era mucho más grande de lo que se pensaba, al demostrar que las llamadas "nebulosas espirales" no eran nubes de polvo y gas como se creía hasta entonces, sino galaxias más allá de la nuestra.

En pocos años, la idea de un universo restringido a la Vía Láctea fue sustituida por la de un vasto espacio lleno de galaxias, donde la nuestra es solo una más. Con ello, además, se expandió radicalmente la escala del cosmos y se abrió el camino a otras investigaciones que culminaron con la formulación de la Ley de Hubble, que describe la expansión del universo y es actualmente uno de los pilares de la cosmología moderna, sentando en su momento las bases para el desarrollo de la teoría del Big Bang.

A pesar de que Hubble es, como científico, relativamente desconocido fuera de la academia, su trabajo transformó de manera radical y definitiva nuestra visión del cosmos y del lugar que los seres humanos ocupamos en él, lo que lo convierte, de hecho, en uno de los investigadores con mayor impacto social de todos los tiempos.

5. Chen-Ning Yang (1922-), Tsung-Dao Lee (1926-2024) y Chien-Shiung Wu (1912-1997)

El hoy conocido como experimento de Wu fue llevado a cabo por un equipo del Grupo de Baja Temperatura del Instituto Nacional de Estándares de Estados Unidos, bajo su dirección, en diciembre de 1956. Durante el experimento, Wu y su equipo observaron la desintegración de átomos de cobalto-60 con los spines alineados en una dirección específica. Al desintegrarse, el átomo de cobalto se rompe, dando como resultado un átomo de níquel, un electrón, un antineutrino y dos fotones. El foco del experimento estuvo en los electrones, pues en caso de conservarse la paridad, estos debían ser emitidos por igual a favor y en contra de la dirección del spin de los átomos de cobalto.

De manera intuitiva, uno pensaría que la reflexión de un sistema en un espejo es una operación demasiado inocente como para afectar las leyes físicas que lo rigen. Pero por eso mismo, Yang y Lee encontraban tan extraña esa ausencia de evidencias de que esta operación no afectaba a los sistemas regidos por la interacción débil. Con esta incógnita en mente, se dirigieron a su compatriota Chien-Shiung Wu, exmiembro del Proyecto Manhattan, experta en espectroscopía del decaimiento beta y una de las físicas experimentales más respetadas e importantes de todos los tiempos, para que los ayudara a diseñar un experimento que permitiera discernir si la paridad se conservaba o no en el decaimiento radiactivo.

Al contrario de lo esperado, se halló que los electrones eran emitidos preferencialmente a favor de la dirección del spin, demostrando la no conservación de la paridad en la interacción débil. Esto sorprendió enormemente a la comunidad científica y no fue aceptado de inmediato, ya que muchos investigadores creían que se trataba de un error experimental. Sin embargo, el experimento fue repetido, y una vez que se estableció que los resultados eran correctos, la no conservación de la simetría de paridad en la interacción débil se ha revelado como un hecho crucial y aún incomprendido dentro de la física de partículas, estando relacionado con algunas de sus predicciones más extraordinarias, como la existencia de la mal llamada "partícula de Dios", o sea, el bosón de Higgs, y con otros fenómenos aún no del todo comprendidos, como la asimetría materia-antimateria (el hecho de que haya más materia que antimateria en el universo) y la posible existencia de partículas aún no detectadas, como aquellas que podrían constituir la materia oscura.

6. Fritz Zwicky (1898-1974), Vera Rubin (1928-2016) y Kent Ford (1931-2023)

El astrónomo y físico búlgaro Fritz Zwicky se hizo conocido mientras trabajaba en el Instituto de Tecnología de California (Caltech) por su enfoque poco convencional y sus ideas innovadoras. Entre ellas, la propuesta en 1933 de la existencia de un tipo de materia desconocida. Zwicky estaba estudiando el cúmulo de galaxias de Coma y observó que la masa visible no era suficiente para explicar las velocidades de las galaxias dentro del cúmulo, infiriendo de ello la existencia de un tipo de materia que los telescopios no eran capaces de detectar. A esta materia se le llamó posteriormente “oscura”, ya que ella no emite o absorbe luz en cantidad suficiente como para ser detectada por los aparatos de observación astronómica convencionales, y solo es posible saber de su existencia de manera indirecta, a través de sus efectos gravitacionales.

Por otra parte, también existe la posibilidad de que la aparente existencia de la materia oscura no sea más que una mala interpretación de las observaciones astronómicas, y que lo que se requiera sea una corrección o generalización de nuestras teorías actuales, en lugar del hallazgo de un nuevo tipo de partícula. Esto ha convertido al problema de la materia oscura en una de las interrogantes cruciales de la física contemporánea, cuya solución, cualquiera que sea, se espera que produzca en los próximos años una verdadera revolución, abriendo, de una forma u otra, el camino hacia nuevos fenómenos que no alcanzamos a imaginar.

La alemana Emmy Noether, conocida como la “madre del álgebra abstracta” y considerada uno de los grandes matemáticos del siglo XX al ser una figura clave en el desarrollo moderno de esta ciencia, fue contactada en 1915 por el matemático David Hilbert para que lo ayudara con un problema que este había encontrado en la Teoría de la Relatividad General (TRG). Resulta que de acuerdo con los estudios de Hilbert, la TRG incumplía el principio de conservación de la energía, una de las bases fundacionales de la física. Emmy se unió con Hilbert en Göttingen en 1915 y en 1918 publicó la demostración de lo que hoy se conoce como Primer Teorema de Noether o, para los físicos, simplemente el teorema de Noether, que establece que, dado un sistema físico, a toda simetría continua le corresponde una magnitud conservada; lo que en términos simples significa que si un sistema es simétrico (como un objeto que se ve igual al girarlo sobre sí mismo), existe una de sus propiedades, determinada por esa simetría, que no cambia.

El teorema de Noether no solo permite probar que la energía sí se conserva en la TRG, sino que constituye una herramienta matemática para determinar las leyes de conservación de cualquier sistema, o sea, para determinar aquellas magnitudes físicas que no cambian en el tiempo y que por tanto lo caracterizan de manera absoluta. Por ejemplo, si un sistema físico no se modifica ante traslaciones en el espacio (simetría traslacional), pues en él se conserva la cantidad de movimiento lineal, mientras que si no cambia al rotar (simetría de rotación) pues en él se conserva la cantidad de movimiento angular. Simetrías más complejas desde un punto de vista matemático en el espacio-tiempo conducen a la conservación de la energía, de la carga eléctrica o del número de partículas.

Una metodología similar desarrolló en la década de 1830 el irlandés William Rowan Hamilton (1805-1865, Dublín), pero en su reformulación, el papel central que ocupaba la fuerza en la teoría de Newton fue reemplazado por la energía total, expresada a través de lo que hoy se conoce como el hamiltoniano del sistema. Hamilton fue un niño prodigio que se destacó en matemáticas y lenguas desde muy joven, y cuyo trabajo abarcó muchas áreas de la física, además de la mecánica.

Giuseppe Lodovico Lagrangia, más conocido por su nombre en francés, Joseph-Louis Lagrange, nació en Turín, actual Italia, en 1736. Allí estudió matemáticas, aunque posteriormente se estableció en París, donde murió en 1813. En su libro Mecánica Analítica, publicado en 1788, Lagrange plantea una reformulación matemática de la Mecánica Clásica (la de Newton), en la que, en lugar de describir el movimiento de los objetos a partir del concepto de fuerza, los conceptos de energía cinética y potencial, combinados en lo que hoy conocemos como el lagrangiano del sistema, pasan a ocupar el lugar central.

4. Edwin Hubble (1889, Marshfield, Misuri -1953, San Marino, California)

Entre los años 1923 y 1924, utilizando el telescopio Hooker, uno de los más potentes de la época, Hubble fue capaz de identificar estrellas individuales, las Cefeidas, dentro de la llamada nebulosa de Andrómeda. La identificación de estas estrellas permitió a Hubble calcular la distancia entre la Tierra y dicha nebulosa, descubriendo que esta se encontraba a más de dos millones de años luz, es decir, mucho más lejos que cualquier otra estrella de la Vía Láctea, y demostrando no solo que dicha nebulosa no estaba dentro de nuestra galaxia, sino que ella misma era una galaxia aparte, con un tamaño comparable al de la nuestra.

Los físicos chinos Chen-Ning Yang y Tsung-Dao Lee se habían trasladado a Estados Unidos con el fin de dedicarse a la física de partículas, y estaban en ello cuando en 1956, tras una extensa revisión bibliográfica, notaron que, a diferencia de lo que sucedía con el resto de las fuerzas de la naturaleza, en el caso de la interacción débil (la que rige la desintegración radiactiva de los núcleos atómicos), la conservación de la simetría de paridad parecía no haber sido probada ni teórica ni experimentalmente.

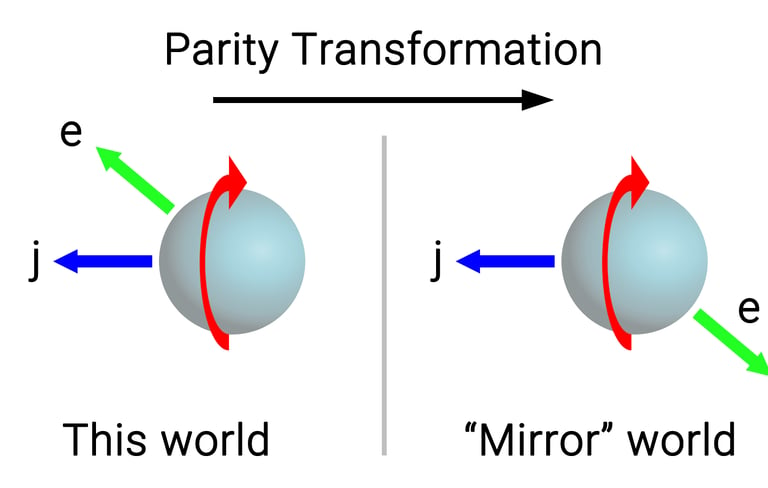
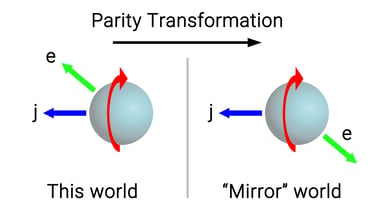
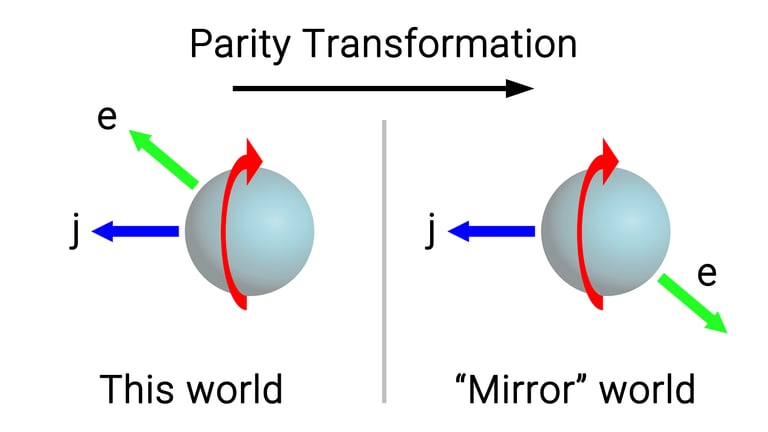
Se dice que un sistema físico tiene simetría de paridad si las leyes que lo rigen no cambian al invertir el signo de las coordenadas espaciales. El intercambio del signo de las coordenadas espaciales es equivalente a la inversión que sufre nuestra imagen reflejada en un espejo, donde, por ejemplo, nuestra mano izquierda se convierte en la derecha y viceversa. Así, un sistema o experimento tiene simetría de paridad si, al ser reflejado en un espejo, se comporta igual que en el mundo real.

Aunque esto puede parecer confuso, el truco está en que, al ser reflejado en un espejo, la dirección y sentido del spin (j) no cambian, pero la de los electrones (e) sí. Por tanto, si en el sistema real los electrones se mueven solo a favor del spin, en el sistema reflejado se moverán solo en la dirección contraria, de manera que ambos experimentos no serían equivalentes, porque uno podría siempre saber cuál es el real (en el que los electrones se mueven a favor del spin) y cuál el reflejado (en el que se mueven en contra).

Con los datos de Tycho, Kepler se dio a la tarea de demostrar que Marte se movía alrededor del Sol describiendo una curva cerrada, específicamente una circunferencia, ya que, a su entender, esta era la curva más elegante y simple. No obstante, luego de cinco años de intentos fallidos, decidió probar con otras curvas, o combinaciones de estas, hasta concluir en 1609 que el mejor ajuste posible entre los datos y su representación matemática se lograba al suponer que Marte se movía alrededor del Sol describiendo una elipse (una elipse es como un círculo alargado, como la forma de un óvalo o una pista de carreras). Esta conclusión le permitió plantear sus tres leyes del movimiento planetario, también conocidas como Leyes de Kepler, que relacionan las características geométricas de la órbita (su longitud, sus radios máximo y mínimo, su área, etc.) con las del movimiento del planeta que la describe (velocidad, tiempo que demora en dar una vuelta, etc.), conectando de manera definitiva lo que hasta entonces se consideraban disciplinas distintas: la astronomía, que era una rama de la matemática, y la física, que se veía como parte de la filosofía.

Sin embargo, la idea de la existencia de esta materia "oscura" no ganó mucha popularidad hasta las observaciones de los astrónomos estadounidenses Vera Rubin y Kent Ford en la década de 1970. Ellos llegaron a la misma conclusión que Zwicky acerca de la existencia de cierta materia no detectada, al descubrir que las velocidades de rotación de las estrellas en las galaxias espirales no disminuyen con su distancia al centro de la galaxia, como se esperaría según las leyes de Kepler, si estas se aplican teniendo en cuenta la masa visible de la galaxia, observada a través de sus emisiones de ondas electromagnéticas.

Las observaciones de Rubin y Ford establecieron de manera definitiva la idea de Zwicky acerca de la existencia de un tipo de materia desconocida en el universo, una idea que se ha convertido en parte fundamental de la cosmología moderna y en uno de los problemas más complejos de la física. Aunque hoy en día existen cientos de partículas hipotéticas que son candidatas a ser materia oscura, así como múltiples experimentos y observatorios, como el Observatorio de Rayos Cósmicos Pierre Auger y el Gran Colisionador de Hadrones (LHC) en el CERN, diseñados para detectar partículas de materia oscura y entender su naturaleza, hasta ahora ninguna otra propiedad de esta materia ha podido ser medida más allá de su efecto gravitacional